Band limit
Band limit
V1.40 , Periodic waveforms other than sine waves generated simple graphical waveforms.
This is useful for testing hardware and software, as a modulation signal, but it was not correct for use (listening) as a voice signal.
It generates so-called aliasing (folding noise, aliasing) because it contains components above the sampling frequency / 2 (Nyquist frequency) that should not be present as an audio signal.
Beginning with V1.50, band-limited periodic waveforms without them ( square wave , triangle wave , sawtooth wave , pulse , pulse (+ -) ).
When using it as an audio signal, please use this band-limited waveform.
In order to generate band-limited periodic waveforms, band limit combo box of Wave 1 or Wave 5![]() None Set it other than.
None Set it other than.
Currently, it is possible to use two kinds of addition synthesis (Additive Synthesis) and BLIT synthesis (Band Limited Impulse Train Synthesis).
![]()
* Although it does not synthesize, even if you are generating a sine wave, if you set the band limit combo box to something other than none , no signal will be output if you set a frequency above the Nyquist frequency.
* Since the amplitude is increased by the vibration waveform due to the so-called Gibbs phenomenon compared to the signal which is not band-limited in the band-limited signal, when the amplitude setting is generated at 0 dB, the level is normally over.
Therefore it is good to keep it to about -3 dB.
|
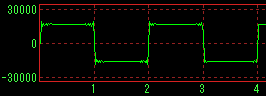
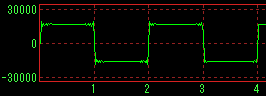
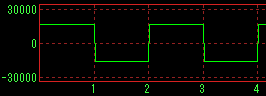
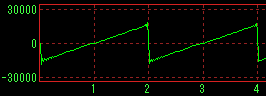
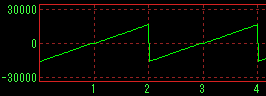
With band limit |
|
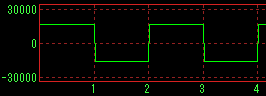
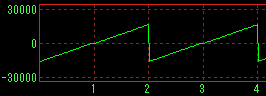
No band limit |
|
|
|
|
|
|
|
|
Especially when sweeping, it is necessary to lower it further for the reason of Note below.
* It is possible to sweep even band-limiting signals and change the duty cycle by PWM.
(Changing duty cycle is only for BLIT synthesis)
However, the following cautions are necessary.
note:
When the frequency of the band limit signal is continuously changed, amplitude discontinuity occurs because the harmonic (harmonic) component suddenly disappears (increases).
Particularly in the case of BLIT synthesis, because the amplitude of the band limitation pulse becomes discontinuous and integrating it, it is possible that the waveform jumps greatly depending on the condition (shock sound may be generated depending on circumstances) depending on the condition please.
Addition synthesis
- Additive synthesis is a method of adding literally harmonic (harmonic) components up to the Nyquist frequency of that waveform and synthesizing them.
It approximates by Fourier series expansion of the waveform.
Accurate synthesis is possible, but if the fundamental frequency is low, the number of components to be synthesized will be large, so it will take much computation time. - Combining formulas for each waveform with the amplitude correction value omitted is as follows.
Rectangular wave:
sin(x) + 1/3 * sin(3x) + 1/5 * sin(5x) + 1/7 * sin(7x) ...
Triangular wave:
cos(x) + 1/9 * cos(3x) + 1/25 * cos(5x) + 1/49 * cos(7x) ...
Sawtooth wave:
sin(x) + 1/2 * sin(2x) + 1/3 * sin(3x) + 1/4 * sin(4x) ...
pulse:
cos(x) + cos(2x) + cos(3x) + cos(4x) ...
Pulse (+ -):
cos(x) + cos(3x) + cos(5x) {cos(7x) ...
note:
You can not change the duty cycle by PWM by adding synthesis.
Also, there are differences in starting point between other waveforms in square wave and sawtooth wave.
(Please see the bottom difference in starting point of addition synthesis - In consideration of computation time and practical accuracy, we currently synthesize harmonics up to the 1000th order.
(It is up to the 1000th even with rectangular waves including only odd harmonics.)
Therefore, if the fundamental frequency is 20 Hz, harmonics up to 20 kHz will be synthesized.
If the sampling frequency is 48 kHz, there are bands up to 24 kHz, but only 20 kHz is synthesized.
In the case of sounding in real time, if the CPU is not powerful, it may take time to calculate if it is a very low frequency and sound skipping will occur.
In that case please write it to the wave file once and use it.
(Currently the program is not particularly speeded up, but it may be faster in the future)
BLIT synthesis
- BLIT synthesis is a method of creating a band-limited impulse train (Band Limited Impulse Train), integrating it and synthesizing the waveform.
Since the band-limited impulse is used, the synthesized waveform is also band-limited.
However, because there are fundamental errors due to the fact that the amplitude of the pulse is constant and unchanged, and instability to integrate, although the harmonic number included in the band limitation pulse varies depending on the synthesized frequency, Is inferior in terms of error and stability.
It may become unstable when sweeping or when the duty cycle is not 50%.
However, since the calculation time is the same regardless of the fundamental frequency, it is different from addition synthesis. Even when the fundamental frequency is very low, it is possible to synthesize signals containing all the harmonics in the band. - Pulse and pulse (+ -):
These are created directly as positive and negative BLIT.
Rectangular wave:
Integrating alternating + - impulses (and removing the DC component) produces a square wave.
(Actually, for sake of stability when changing the duty cycle, sawtooth wave with different phase from positive and negative pulses is created, and the difference is taken as a rectangular wave.)
Triangular wave:
A triangle wave is obtained by integrating the rectangular wave again.
Sawtooth wave:
Integrating a positive pulse train with a negative constant proportional to the cycle produces a sawtooth wave.
* The duty cycle can be changed by PWM for square wave, triangle wave, pulse (+ -). - note:
As mentioned above, this method creates waveforms using integration, so it may become unstable depending on conditions.
(The waveform goes somewhere)
Although devised so as to make stability and waveform accuracy compatible by correction and incomplete integration by an appropriate time constant, depending on the correction of the difference in the amplitude of the pulse by the fundamental frequency, it is inevitably unstable depending on the initial value of the integration It may become.
When sweeping, stability is improved by decreasing the time constant of incomplete integration, but the waveform slightly distorts by that amount.
(Tilt it)
Even when not sweeping, it is difficult to obtain an accurate initial value in principle when the duty cycle is set to something other than 50%, so the waveform may jump greatly at the start.
In that case just a few need be enough, please change the duty cycle or fundamental frequency.
In most cases this should be solved. - References:
Alias-Free Digital Synthesis of Classic Analog Waveforms
[Tim Stilson, Julius Smith, Music Department, Stanford University]
https://ccrma.stanford.edu/~stilti/papers/blit.pdf
Difference in starting point of addition synthesis
- In addition synthesis, the start point differs from other waveforms, "zero" It starts from the point of. (1 sample different)
|
|
Addition synthesis |
|
BLIT synthesis |
|
No band limit |
|
Square wave |
|
|
|
|
|
|
Sawtooth wave |
|
|
|
|
|
Created with the Personal Edition of HelpNDoc: Easily create iPhone documentation